| The Rational Function Model: A Tool for Processing High-resolution Imagery
By C. Vincent Tao and Yong Hu Physical sensor models and generalized sensor models
Sensor models are required to rectify the functional relationships between the image space and the object space, and are of particular importance in image ortho-rectification and stereo intersection. There are two categories of sensor models; physical sensor models, and generalized sensor models.
A physical sensor model represents the physical imaging process. The parameters involved describe the position and orientation of a sensor with respect to an object-space coordinate system. The physical models are rigorous, such as with collinearity equations, and are very suitable for adjustment by analytical triangulation and normally yield high modeling accuracy within a fraction of one pixel. In physical models, parameters are statistically uncorrelated, as each parameter has a physical significance.
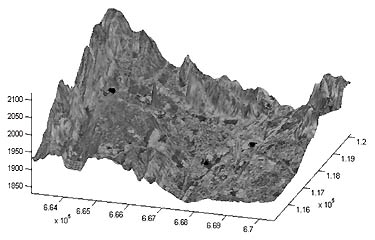 The ortho-rectified image draped on a DEM (Figure 1) The ortho-rectified image draped on a DEM (Figure 1) Physical sensor models are sensor-dependent, i.e., different types of sensor need different models. With the increasing availability of new airborne and space-borne sensors, and the wide use of different types of sensors such as Frame, Pushbroom, Whiskbroom, Panoramic, and SAR, from an application point of view it is not convenient for users to change software or add new sensor models into their existing system for processing new sensor data. It has also been realized that rigorous physical sensor models are not always available, especially for images from commercial satellites (e.g. IKONOS). Without knowing its imaging parameters such as orbit parameters, sensor platforms, ephemeris data, relief displacement, Earth curvature, atmospheric refraction, lens distortion, etc., it would be difficult to develop a rigorous physical sensor model.
Development of generalized sensor models independent of sensor platforms and sensors becomes attractive due to the above reasons. In a generalized sensor model, the transformation between object and image space is represented as some general function, without modeling the physical imaging process. The function can be in several different forms, such as polynomials. In general, generalized sensor models do not require knowledge of the sensor geometry, thus they are applicable to different sensor types.
Use of generalized sensor models to replace rigorous physical sensor models has been in practice for a decade. It was used initially for U.S military intelligence applications, wherever physical sensor models were not available or when real-time calculation was essential. This approach has also been implemented in some of the digital photogrammetric systems (Madani, ZI Imaging). The primary purpose of the use of so-called replacement models is their capacity for sensor independence and support of real-time calculations. Rational Function Model (RFM)
The Rational Function Model (RFM) has gained considerable interest recently among the photogrammetry and remote sensing community. This is mainly due to the fact that some satellite data vendors, for example Space Imaging (Thornton, Colo.), have adopted the RFM as a replacement sensor model for image exploitation. The data vendor will supply users with parameters of the RFM instead of the rigorous sensor models. Such a strategy may help keep information about the sensors confidential and, on the other hand, facilitates the use of high-resolution satellite imagery for general public users (non-photogrammetrists), since the RFM is easy to use and easy to understand.
The rational function model is essentially a generic form of polynomials. It defines the formulation between a ground point and the corresponding image point as ratios of polynomials where rn and cn are the normalized row and column index of pixels in image respectively, and Xn, Yn and Zn are normalized coordinate values of object points in ground space. All four polynomials are functions of the three ground coordinates.
In general, distortions caused by optical projection can be corrected by ratios of first-order terms, and corrections to Earth curvature, atmospheric refraction, and lens distortion, etc., can be well approximated by second-order terms. Some other unknown distortions with high-order components can be modeled with third-order terms. Solving RFM-Terrain Independent vs. Dependent Computational Scenarios
The unknown parameters involved in the RFM can be determined with or without knowing the rigorous sensor models. We therefore present two computational scenarios and compare their results. If a rigorous sensor model is available, the terrain-independent solution can be applied. Otherwise, the RFM solution will be dependent on the input control points that are derived from a terrain model. Terrain-Independent Computational Scenarios
If the rigorous sensor model is available, the RFM can be solved using a 3-D object grid, with its grid-point coordinates determined by using a rigorous sensor model. This solution is, in fact, independent of real terrain since no terrain information is required. This method involves the following steps (see Figure 3):
• Determination of a grid of sufficient image points. The grid contains points. These points are evenly distributed across the full extent of the image. The rows and columns often number around 10.
• Set-up of a 3-D grid of points in ground space. The rigorous sensor model is used to compute the corresponding object positions of the grid points on the image. Therefore, the dimension of this 3-D grid is based on the full extent of the image, and the range of the estimated terrain relief, i.e. the dimension of the grid covers the range of the 3-D terrain surface. The grid contains several elevation layers, and the points on one layer have the same elevation value. To avoid an ill-conditioned design matrix, the number of layers should be greater than three.
• RFM fitting. The RFM is used to fit the 3-D object grid, and the unknowns are solved using the corresponding image and object grid points.
• Accuracy checking. Another 3-D object grid can be generated in a similar manner, but with double density in each dimension. The corresponding image positions of these checkpoints are calculated using the rigorous sensor model. The obtained RFM is then used to calculate the image positions of the object grid points. By calculating the difference between the coordinates of the original grid of image points and those calculated from the RFM, the accuracy of the established RFM can be evaluated. Terrain-Dependent Computational Scenarios
With no rigorous sensor models at hand, corresponding image points of ground points of a 3-D grid cannot be computed. In order to solve for the unknowns, one has to measure control points and check points from both the image and the actual DEM or maps. In this case, the solution is heavily dependent upon the actual terrain relief, the number of control points, and the distribution of control points. This method is essentially terrain-dependent. This method has been widely used in remote sensing applications where the rigorous sensor model is far too complicated to develop, or the accuracy requirement is not stringent.
The University of Calgary has developed a software package called "RationalMapper" (Tao and Yong, 1999). This system is based on an iterative least-square RFM solution, as well as a robust bucketing algorithm for automatic selection of ground control points. The software offers a much more robust and stable solution to RFM parameters. The results (both RMS and maximum errors in pixel on image checkpoints), based on four different test data sets, are shown in the table. The Terrain-independent case yields very high-fitting accuracy and also relies upon the number and distribution of ground control points. RFM Applications-Stereo Intersection and Ortho-Rectification
Given the RFM parameters for a stereo image pair, the 3-D ground position of an object point can thus be calculated. "RationalMapper" uses an inverse form to solve the intersection problem iteratively. In principle, if two images with known RFM parameters have an overlap, the positions of ground points in the overlap area can be computed. This implies that stereo intersection or 3-D measurement can be done using two different types of images as long as they have an overlap, for example, one image is IKONOS and the other is aerial photography. It is obvious that the scale difference of two images would decrease the 3-D intersection accuracy, but this technique is of important use for applications where accuracy is not essential.
RFM-based ortho-rectification has also been developed in the "RationalMapper." With an input image and a corresponding DEM, "RationalMapper" can generate an ortho-rectified image (see Figure 1, where an ortho-rectified image has been draped on a DEM).
We are now developing an Internet based client/server system for RationalMapper. An initial web interface of the "RationalMapper" is shown in Figure 2. This would allow any user to access the system through web browsers (http://geomaci.geomatics.ucalgary.ca/projects/RationalMapper.html). The user could then measure conjugate point pairs from both left and right images, and the system will calculate the 3-D position. This tool would be extremely useful for many applications where 3-D information of some objects (landmarks, or even geological structures) is required. The advantage of such a system is that users do not need photogrammetry training and experience, nor must they purchase sophisticated photogrammetric systems. Comments on RFM
Tendency toward oscillation is a well-known issue in using conventional polynomials for approximation. This often causes error bounds in polynomial approximations that significantly exceed the average approximation error, while RFM (ratios of polynomials) has better interpolation properties. RFM is typically smoother and can spread the approximation error more evenly between exact-fit points. Moreover, rational function has the added advantage of permitting efficient approximation of functions that have infinite discontinuities near to, but outside, the interval of fitting, whereas polynomial approximation is generally unacceptable in this situation.
RFM is independent on sensors or platforms that are involved. It supports any object-space coordinate system such as geocentric, geographic, or any map projection coordinate system. However, compared to those rigorous sensor models, RFM is not suitable for direct adjustment by analytical triangulation.
With adequate control information, RFM can achieve a very high-fitting accuracy. Therefore, one could use a rigorous sensor model to generate a dense grid of control points, thereby using this grid to solve unknown parameters involved in RFM. On the other hand, since there is no functional relationships between the parameters of the rigorous model and those of RFM, physical parameters cannot be recovered from the RFM, and thus the information regarding the physical sensor models can be protected. Due to the two aforementioned reasons, some commercial satellite data vendors, such as Space Imaging Inc., provide users with RFM parameters but do not provide any information regarding physical sensor models. As a result, users are still able to achieve a reasonable accuracy level without knowing the rigorous sensor models.
One of the most attractive features of RFM is that users do not have to change their software system in order to process images. Therefore, one system can be used to processing various types of imagery for stereo intersection and ortho-rectification as long as the RFM parameters of images are provided. An important note here is that it would greatly facilitate users and developers if data vendors could suppler RFM parameters in a common and standard format (an image transformation format). About the Authors:
C. Vincent Tao, Ph.D., P.Eng., is assistant professor in the department of geomatics engineering at the University of Calgary, Canada. His research interests include Internet and wireless GIS; ubiquitous geocomputing, digital photogrammetry, and Lidar and SAR data processing. He is a recipient of many international awards and holds a number of important positions in international working groups in this field, plus editorial positions in geomatics journals. He is a registered professional engineer and certified mapping scientist in photogrammetry. He can be reached via e-mail at [email protected] or by phone at (403) 220-5826.
Dr. Yong Hu is a research assistant in the same department. His research interests include computer vision, image processing, remote sensing, and GIS. He can be reached via e-mail at [email protected] or by phone at (403) 220-8149. Back |




